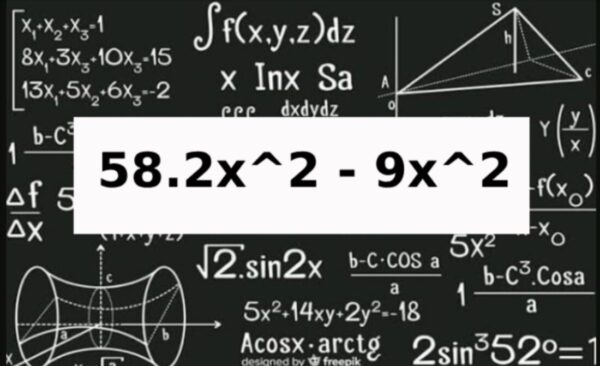In algebra of Mathematics, we use expressions to help us understand math. One expression that can be confusing is “58: 2x^2 – 9x^2; 5 – 3x + y + 6.” We’re going to take a closer look at this expression, break it down into smaller parts, make it simpler, and solve it step by step. By the end, you’ll understand what this expression means and how it can be used.
Also Read: x2+(y-3√2x)2=1
Introduction of Mathematical Equation : 58.2x^2 – 9x^2; 5 – 3x + y + 6
Let’s solve the math problem by putting together the numbers and letters in the expression: 58:2 times x squared minus 9 times x squared, then add 5 minus 3 times x plus y plus 6 ( 58.2x^2 – 9x^2; 5 – 3x + y + 6 ).
Before simplifying the given expression, let’s understand its structure. The Mathematical Equation
contain two parts separated by a semicolon. The first part is “2x^2 – 9x^2” and the second part is “5 – 3x + y + 6“.
Let’s look at the numbers 2 and 9 times the letter “x” squared, and then subtract them from each other.
Breaking Down the Expression
Part 1: 2x^2 – 9x^2
In this part, we are going to talk about the first part of the math problem, “2 times x squared minus 9 times x squared.” The math problem has two parts: “2 times x squared” and “-9 times x squared.” Both parts have the letter x raised to the power of 2. It can be written as 2x^2 – 9x^2.
Part 2: 5 – 3x + y + 6
Imagine you have 5 toys, but then you give away 3 of them. You also have another toy that someone gives you. Finally, you get 6 more toys. So, how many toys do you have in total now? It can be written as 5 – 3x + y + 6.
Simplifying Each Part of the Expression
Now let’s look at the next part of the math problem which is “5 – 3 times x plus y plus 6.” This part also has different pieces like “5,” “-3 times x,” “y,” and “6.” Each piece has a number and some letters.
First, we have 2 of something squared and we need to take away 9 of the same thing squared.
To make it easier, we need to put together the parts that are the same. Both parts have x times x (x^2). When we add 2x^2 and -9x^2, we get -7x^2.
Solving the Expression
To solve the equation, we need to provide a specific value for the variable (x) and evaluate the problem based on that value. Let’s take an example:
Suppose we have x = 3; now, let’s find the value of the expression:
-7(3)^2; 5 – 3(3) + y + 6 = -7(9); 5 – 9 + y + 6 = -63; -4 + y + 6 = -63; 2 + y
Figuring out the answer to a Mathematical Equation problem.
In order to solve the expression, we need to provide a specific value for the variable (x) and evaluate the expression based on that value. for example:
Let’s say we have a number called x, and it is equal to 3. Now, we want to figure out what happens when we use this number in an equation or calculation.
If you multiply 3 by itself and then by 7, subtract 3 times 3 from 5, add a mystery number y and 6, it all equals negative 7 times 9. Then you can solve for the mystery number by following the steps.
Know Practical Applications of Algebraic Expressions
Algebraic expressions can be used in everyday life to solve problems and make things easier. For example, if you want to buy some toys and each toy costs $5, you can use algebra to figure out how much money you need to bring. You can also use algebra to figure out how much time it will take to do your homework if you know how many problems you have to solve and how long it takes to solve each problem. So basically, algebra helps us solve real-life problems and make things go smoothly.
Algebraic expressions are like puzzles that help us solve problems in different subjects like science, math, and technology. They help us figure out how things work in the real world and make predictions. Learning about algebraic expressions is really important for getting better at these subjects.
The ending or final thought.
The math problem “2 times a number squared minus 9 times the same number squared; 5 minus 3 times another number plus a third number plus 6” might seem hard at first. But if we take it apart, simplify each part, and then put it back together, we can understand it better. Also, if we figure out what the numbers are, we can find out what the whole problem equals. Learning about math problems like this is important because they are used in real-life situations.
Also Read: x2-11x+28=0