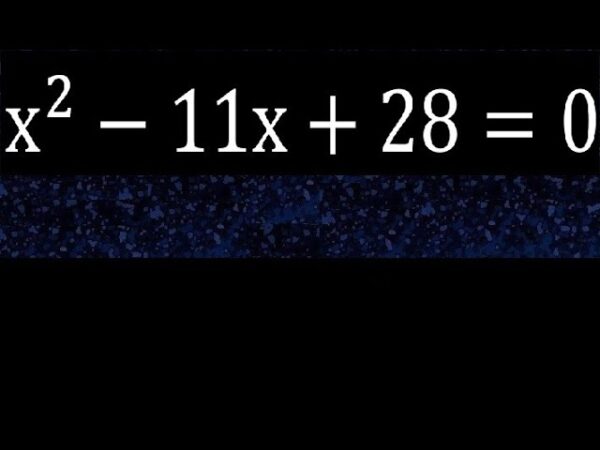x2-11x+28=0 : Quadratic equations are foundational factors within the world of algebra, providing insights into various mathematical and real-world phenomena. Among those, the equation ( x2-11x 28=zero ) stands as a vital instance, showcasing the beauty and intricacy of quadratic answers. This article targets to demystify this particular quadratic equation, supplying a clean expertise of its nature, answers, and programs.
At first glance, ( x2-11x 28=zero ) may also appear as just another mathematical puzzle. However, it holds a good deal more significance. This equation is not best a gateway to gaining knowledge of quadratic equations however also serves as a bridge to knowledge greater complex mathematical ideas. By exploring its solutions, we can benefit insights into the behavior of parabolic features, which find programs in numerous fields which include physics, engineering, and economics.
Our journey through this equation will take us from the fundamentals of quadratic equations to extra advanced principles. We will discover distinctive techniques of fixing this equation, including factorization, the quadratic formula, and completing the rectangular. Each approach offers a unique angle and complements our problem-solving abilities.
Additionally, we are able to delve into the graphical illustration of ( x2-11x 28=0 ), illustrating how the summary translates into the visible. This graphical perspective no longer best aids in know-how the equation’s roots however also presents a deeper appreciation of the properties of quadratic functions, including symmetry and vertex vicinity.
By the end of this newsletter, you may not only be capable of solve (x2-11x 28=0 ) readily but additionally recognize its broader implications in arithmetic and past. Whether you’re a scholar, educator, or actually a curious mind, this exploration promises to enhance your expertise of one in every of algebra’s maximum exciting topics. Let’s embark on this mathematical adventure together, unraveling the mysteries hidden within ( x2-11x 28=0 ).
Background on Quadratic Equations
As a professor delving into the captivating global of quadratic equations, it is important to set up a sturdy foundational know-how of these equations. A quadratic equation is a second-degree polynomial equation of the form ( ax^2 bx c = zero ), where ( a ), ( b ), and ( c ) are constants, and ( a neq zero ). The solution of these equations is essential in diverse mathematical and scientific fields.
Historical Perspective
The have a look at of quadratic equations dates back to historic civilizations, along with the Babylonians, Greeks, and Indians. The strategies and answers developed over centuries have extensively contributed to the development of algebra. Quadratic equations had been most of the first to be solved algebraically, marking a sizeable milestone in the records of mathematics.
General Characteristics
Degree: Quadratic equations are characterized by their maximum electricity, that’s two. This is what differentiates them from linear (first-degree) and cubic (1/3-diploma) equations.
Standard Form: The maximum diagnosed form of a quadratic equation is ( ax^2 bx c = 0 ). However, it is able to additionally be represented in different kinds like vertex form or factored shape, depending at the application.
Coefficients: The coefficients ( a ), ( b ), and ( c ) play important roles in determining the character of the equation’s graph and roots. The coefficient ( a ) affects the parabola’s beginning course and width.
The Parabola
Graphical Representation: When plotted on a graph, quadratic equations form a parabola, a U-formed curve. The direction (upwards or downwards) of the parabola is determined with the aid of the sign of ( a ).
Vertex and Axis of Symmetry: The vertex is the very best or lowest point on the parabola, and the axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetrical halves.
Intercepts: Quadratic equations may also have zero, one, or x-intercepts (roots), and one y-intercept.
Roots of Quadratic Equations
The roots of a quadratic equation are the values of ( x ) that satisfy the equation. They constitute the points where the parabola intersects the x-axis. There are several strategies to find those roots, together with:
Factorization: Expressing the quadratic equation as a made from binomials.
Quadratic Formula: A generic technique that uses the coefficients ( a ), ( b ), and ( c ) to locate the roots.
Completing the Square: Transforming the equation into a super rectangular trinomial.
Discriminant
The discriminant of a quadratic equation, denoted as ( Delta ) and calculated as ( b^2 – 4ac ), offers crucial statistics about the character of the roots:
- Positive Discriminant: Indicates two wonderful real roots.
- Zero Discriminant: Indicates one actual root (a repeated root).
- Negative Discriminant: Indicates complex roots.
Applications
Quadratic equations are not simply theoretical constructs; they have realistic packages in numerous fields:
Physics: Describing projectile movement, loose fall, and different phenomena.
Engineering: Designing structures, analyzing forces, and optimization problems.
Economics: Modeling fee capabilities, sales capabilities, and marketplace equilibrium analysis.
In end, expertise quadratic equations isn’t just about fixing for ( x ); it’s about comprehending a fundamental idea that bridges various disciplines. The equation ( x2-11x 28=0 ) is a classic example that encapsulates these types of elements, serving as an ideal specimen for our exploration.
Solving the Equation x2-11x 28=0
As a professor exploring the intricacies of quadratic equations, let’s dive into the specific methods of solving the unique equation ( x2-11x 28=zero ). This equation, at the same time as reputedly simple, offers a wealthy context for knowledge the diverse techniques used in solving quadratic equations.
1. Factorization Method
The first method is to factorize the quadratic equation. Factorization entails expressing the quadratic equation as a made of binomials.
Step 1: Look for 2 numbers that multiply to ( c ) (that’s 28 in our case) and upload as much as ( b ) (which is -eleven). In this equation, the ones numbers are -four and -7, when you consider that ((-4) instances (-7) = 28) and ((-four) (-7) = -eleven).
Step 2: Rewrite the equation as ( (x – four)(x – 7) = 0 ).
Step three: Set every component same to 0: ( x – four = 0 ) and ( x – 7 = 0 ).
Step 4: Solve for ( x ) in each case, yielding the roots ( x = four ) and ( x = 7 ).
2. Quadratic Formula
The quadratic components is a conventional method that can be used to discover the roots of any quadratic equation. The formulation is ( x = frac-b pm sqrtb^2 – 4ac2a ).
Step 1: Identify ( a ), ( b ), and ( c ) from the equation. Here, ( a = 1 ), ( b = -11 ), and ( c = 28 ).
Step 2: Plug those values into the quadratic formulation: ( x = frac-(-eleven) pm sqrt(-eleven)^2 – 4 cdot 1 cdot 282 cdot 1 ).
Step 3: Simplify below the rectangular root: ( x = frac11 pm sqrt121 – 1122 ).
Step 4: Further simplify: ( x = fraceleven pm sqrtnine2 ).
Step 5: Solve for ( x ), giving answers: ( x = fraceleven pm three2 ), which can be ( x = four ) and ( x = 7 ).
3. Completing the Square
Completing the square is a way that includes reworking the quadratic equation into an excellent rectangular trinomial.
Step 1: Rewrite the equation inside the form ( x^2 bx = -c ). For our equation, it turns into ( x^2 – 11x = -28 ).
Step 2: Add (left(fracb2proper)^2) to both sides. Here, ( b = -eleven ), so (left(frac-eleven2proper)^2 = 30.25). The equation will become ( x^2 – 11x 30.25 = 2.25 ).
Step 3: Rewrite the left side as a squared binomial: ( (x – five.5)^2 = 2.25 ).
Step 4: Take the rectangular root of both aspects: ( x – 5.5 = pm sqrt2.25 ).
Step 5: Solve for ( x ), resulting in ( x = five.Five pm 1.Five ), which gives ( x = four ) and ( x = 7 ).
Applications of the Quadratic Equation ( x2-11x 28=0 )
As a professor inspecting the quadratic equation (x2-11x 28=zero ), it’s far critical to discover its applications beyond the classroom. This equation, at the same time as a simple mathematical expression, may be a version for diverse actual-global phenomena. Understanding those programs now not best enriches the getting to know enjoy but also showcases the sensible application of quadratic equations.
1. Physics and Engineering
In physics, quadratic equations often stand up in the context of projectile motion and kinematics. For example, the equation ( x2-11x 28=zero ) can represent a scenario in projectile motion wherein ( x ) ought to characterize the time elapsed, and the equation gives precise instances when the projectile reaches sure heights or distances.
In engineering, such equations are critical in designing parabolic paths or structures. The parameters of the equation can represent dimensions or forces acting on a shape, supplying insights into choicest layout and balance.
2. Economics and Business
In the sphere of economics, quadratic equations can be used to version price, sales, or income capabilities. The roots of the equation ( x2-11x 28=0 ) would possibly represent smash-even factors in a commercial enterprise version, in which revenue equals cost, indicating no income or loss.
Similarly, in investment analysis, such equations can help in figuring out the maximum income or loss, or the conditions under which a positive go back on investment is completed.
3. Biology and Environmental Science
Quadratic equations have their area in biology for modeling population dynamics or the unfold of diseases. The equation ( x2-11x 28=0) could, as an instance, represent a model in which the populace size or the range of inflamed people is a function of time or another variable.
In environmental technological know-how, such equations may be used to model boom styles of flowers or the spread of pollution beneath positive situations.
4. Optimization Problems
Quadratic equations are indispensable in fixing optimization issues throughout diverse fields. For example, in logistics and operations, the equation ( x^2 – 11x 28 = zero ) may be a part of a larger model to minimize charges or maximize efficiency in a deliver chain.
5. Art and Architecture
In artwork and structure, the parabolic shapes described by quadratic equations, which includes (x2-11x 28=zero), impact design and aesthetic alternatives. The symmetry and curvature inherent in these equations can guide the creation of visually eye-catching and structurally sound designs.
Conclusion
In exploring the quadratic equation ( x2-11x 28=zero ), we’ve got journeyed thru a landscape rich in mathematical principles and real-global programs. This exploration has no longer best demystified the process of fixing such an equation via various strategies like factorization, the quadratic formulation, and finishing the rectangular however has also illuminated the profound implications of quadratic equations in numerous fields.